幾何變換

當我們在兩張圖片中找到了對應的特徵點後，如何計算出一個能將一張圖片「變形」到另一張圖片視角下的矩陣？這個矩陣稱為單應性矩陣 (homography)，今天則要討論這個矩陣的理論細節。

幾何變換 (geometric transformation) 描述了物體在空間中的移動、旋轉、縮放和形變。在2D影像中，最關鍵的兩種變換是

1. 仿射變換 (affine transform): 保留了線的「平行性」。它只能做到旋轉、縮放、平移和剪切。一個平行四邊形經過仿射變換後，依然是一個平行四邊形。

2. 透視變換 (perspective transform): 這是更通用的變換，它不保留平行性。它能模擬相機從不同視角拍攝物體時產生的「近大遠小」效果。一個正方形經過透視變換後，可能變成任意一個梯形。我們今天要計算的單應性矩陣就是一種透視變換。

匹配特徵點

要計算變換，前提是我們需要一組「對應點」(Correspondences)，在實務上有兩種主流的匹配器 。

BF 匹配

原理非常簡單：拿出第一張圖的每一個描述子，去和第二張圖的所有描述子計算「距離」（例如歐氏距離或漢明距離），然後選擇距離最近的那個作為匹配。它簡單直觀，對於 ORB 這類二進位描述子搭配漢明距離時，速度非常快。

FLANN 匹配

當特徵點數量巨大時（例如 SIFT 產生的數千個特徵點），BF 匹配會變得非常慢。FLANN 使用了像 KD-Tree 或 LSH 等演算法，來進行近似最近鄰搜索。它犧牲了極小的精度，來換取數量級的速度提升，是 SIFT/SURF 等高維描述子的標配。

單應性矩陣

單應性矩陣 H 是一個 3x3 的矩陣，它描述了兩個平面之間的透視變換關係。如果我們知道點 p1 = (x1, y1) 在第一張圖中，以及它對應的點 p2 = (x2, y2) 在第二張圖中，它們的關係可以表示為：

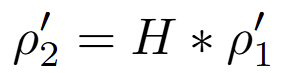
其中 ρ’是齊次座標 (x, y, 1)。這個 3x3 矩陣有8個未知數（自由度）。因此，理論上我們只需要4對不共線的對應點，就可以解出這個矩陣 H。

成本函數

在實務中，我們會使用超過 4 對的點（例如，50 對匹配點）來求解。這時問題就變成了一個最佳化問題：找到一個矩陣 H，使得所有對應點經過 H 變換後的誤差總和最小。這個誤差總和，就是我們的成本函數，通常使用對稱轉移誤差的平方和。

DLT

DLT 是一種直接求解單應性矩陣的經典演算法。它的核心思想是將

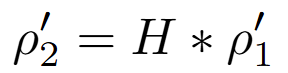
這個非線性關係，透過一些數學技巧，轉換成

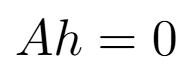
的線性方程組形式。每一對匹配點，都可以提供兩個線性方程式。因此，只要有 4 對點，我們就能湊出 8 個方程式，解出 H 矩陣的 8 個未知數。

非齊次解

Ah = 0 是一個齊次線性方程組。在實務中，由於雜訊的存在，這個方程通常沒有精確解。我們會去尋找一個「最小範數解」，這通常可以透過對矩陣 A 進行奇異值分解 (Singular Value Decomposition, SVD) 來高效地求得。A 的最小奇異值對應的奇異向量，就是我們要求的 h，再將其重塑回 3x3 的矩陣 H 即可。

文件校正

準備一張從歪斜角度拍攝的文件照片，以下程式能將他校正成如同掃描器掃出來的俯瞰視角。

import cv2
import numpy as np

# --- 全域變數 ---
points = [] # 用來儲存點擊的四個點
image = None

def mouse_callback(event, x, y, flags, param):
    """滑鼠回呼函式，用於記錄點擊座標"""
    global points, image
    if event == cv2.EVENT_LBUTTONDOWN:
        if len(points) < 4:
            points.append((x, y))
            # 在圖片上畫出點擊位置
            cv2.circle(image, (x, y), 5, (0, 0, 255), -1)
            cv2.imshow("Original Image - Select 4 Corners", image)
            print(f"已選取 {len(points)} 個點: ({x}, {y})")

def order_points(pts):
    """
    對四個點進行排序，順序為：左上、右上、右下、左下
    """
    rect = np.zeros((4, 2), dtype="float32")
    
    # 左上角的點 x+y 最小，右下角的點 x+y 最大
    s = pts.sum(axis=1)
    rect[0] = pts[np.argmin(s)]
    rect[2] = pts[np.argmax(s)]
    
    # 右上角的點 y-x 最小，左下角的點 y-x 最大
    diff = np.diff(pts, axis=1)
    rect[1] = pts[np.argmin(diff)]
    rect[3] = pts[np.argmax(diff)]
    
    return rect

# --- 主程式 ---
image_path = 'document.jpg'
image = cv2.imread(image_path)

clone = image.copy()
cv2.namedWindow("Original Image - Select 4 Corners")
cv2.setMouseCallback("Original Image - Select 4 Corners", mouse_callback)

print("請按順時針或逆時針，依序點擊文件的四個角點。")
print("選取完畢後，按 'c' 鍵進行校正。")
cv2.imshow("Original Image - Select 4 Corners", image)

key = cv2.waitKey(0)

if key == ord('c') and len(points) == 4:
    # 1. 獲取並排序我們選取的四個源點
    src_points = order_points(np.array(points, dtype="float32"))
    (tl, tr, br, bl) = src_points
    
    # 2. 計算輸出影像的尺寸
    # 寬度是右下/右上與左下/左上 x 座標差值的最大值
    widthA = np.sqrt(((br[0] - bl[0]) ** 2) + ((br[1] - bl[1]) ** 2))
    widthB = np.sqrt(((tr[0] - tl[0]) ** 2) + ((tr[1] - tl[1]) ** 2))
    maxWidth = max(int(widthA), int(widthB))

    # 高度是右上/左上與右下/左下 y 座標差值的最大值
    heightA = np.sqrt(((tr[0] - br[0]) ** 2) + ((tr[1] - br[1]) ** 2))
    heightB = np.sqrt(((tl[0] - bl[0]) ** 2) + ((tl[1] - bl[1]) ** 2))
    maxHeight = max(int(heightA), int(heightB))
    
    # 3. 定義目標影像的四個角點 (一個標準的矩形)
    dst_points = np.array([
        [0, 0],              # 左上
        [maxWidth - 1, 0],   # 右上
        [maxWidth - 1, maxHeight - 1], # 右下
        [0, maxHeight - 1]   # 左下
    ], dtype="float32")
    
    # 4. 計算單應性矩陣 H
    # cv2.getPerspectiveTransform(源點座標, 目標點座標)
    H = cv2.getPerspectiveTransform(src_points, dst_points)
    
    # 5. 應用透視變換
    # cv2.warpPerspective(原始影像, 變換矩陣, (輸出寬, 輸出高))
    warped_image = cv2.warpPerspective(clone, H, (maxWidth, maxHeight))
    
    # 顯示結果
    cv2.imshow("Original Image", clone)
    cv2.imshow("Scanned Result", warped_image)
    cv2.waitKey(0)

cv2.destroyAllWindows()